Quantum Error Correction

Introduction to Quantum Error Correction

In our exciting journey through the quantum realm, we’ve touched on some pretty mind-bending concepts like superposition and entanglement. Today, we're diving into another crucial area that’s essential for the future of quantum computing: Quantum Error Correction (QEC). Think of it as the unsung hero working behind the scenes to ensure our quantum computations stay on track.

The Quantum Error Challenge

In the classical world, computers are pretty robust. Errors happen, but they’re rare and usually easy to fix with straightforward redundancy checks. But in the quantum world, things get trickier. Qubits, the building blocks of quantum computers, are incredibly delicate. They can exist in superpositions, where they are simultaneously in multiple states, and they can be entangled with other qubits. This delicate nature makes them highly susceptible to errors from even the slightest environmental interference, known as decoherence, and quantum noise.

To put it in relatable terms, imagine you're trying to balance a spinning coin on the tip of your finger while walking on a tightrope. Any slight breeze or misstep can throw the coin off balance. In quantum computing, we need a way to keep that coin spinning perfectly despite all the disturbances. That’s where Quantum Error Correction comes in.

Types of Quantum Errors

Quantum errors can be broadly classified into two main types:

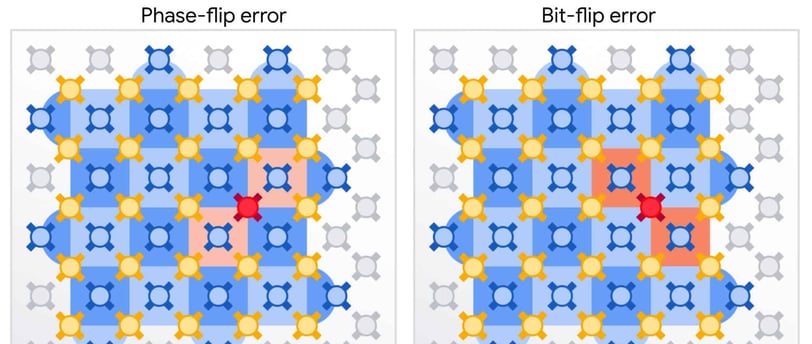
• Bit-flip errors: This is like a classical bit flipping from 0 to 1 or vice versa.

• Phase-flip errors: This type of error affects the phase of the qubit, altering its state in a more subtle way. Imagine it as changing the direction of the spin without flipping the spin itself.

There is also a third type, known as bit-phase flip errors, which are a combination of both bit-flip and phase-flip errors. Both types of errors can derail quantum computations if not corrected promptly.

The Basics of Quantum Error Correction

So, how do we correct these errors without directly measuring the qubits, which would collapse their quantum states? The answer lies in encoding the logical qubit into a higher-dimensional space using multiple physical qubits. This redundancy allows us to detect and correct errors without destroying the quantum information.

One of the pioneering QEC codes is the Shor Code, named after Peter Shor. This code encodes a single logical qubit into nine physical qubits, allowing it to detect and correct both bit-flip and phase-flip errors. Another popular code is the Surface Code, which is particularly promising for scalable quantum computing. The Surface Code uses a 2D grid of qubits and can correct a high rate of errors with relatively fewer resources, making it a strong candidate for practical quantum computers.

How QEC Works: A Deeper Dive

Let's break it down further. Implementing QEC involves two key steps:

1. Error Detection: Using ancillary (extra) qubits and quantum gates, we measure error syndromes that indicate if and where an error has occurred. This process doesn’t collapse the qubit states but provides enough information to identify the error type.

2. Error Correction: Based on the detected syndromes, specific quantum gates are applied to correct the errors and restore the qubits to their intended states.

This process must be performed repeatedly throughout the quantum computation to ensure that the qubits remain error-free.

Quantum Error Correction Codes: Shor Code and Surface Code

Shor Code: The Shor Code is a pioneering quantum error correction code that uses nine physical qubits to encode a single logical qubit. This code can correct both bit-flip and phase-flip errors, offering a robust solution for early quantum computers. The Shor Code works by spreading the information of one logical qubit across multiple physical qubits, creating redundancy that allows for error detection and correction.

Surface Code: The Surface Code is another highly regarded QEC code, particularly suitable for scalable quantum computing. It uses a 2D lattice of qubits, where each qubit is connected to its neighbors. This code can handle a high rate of errors and is designed to work with the physical layout of many current quantum computers. The Surface Code is expected to play a crucial role in the development of fault-tolerant quantum computers.

The Importance of Error Syndromes

Error syndromes are the backbone of Quantum Error Correction. They provide the necessary information to detect errors without directly measuring the qubits. Ancillary qubits, often called "syndrome qubits," interact with the data qubits to capture the error information. This interaction is carefully designed to preserve the quantum state while allowing the error to be identified. Once the error syndromes are measured, the quantum computer can apply the appropriate correction operations to restore the qubits to their correct states.

Practical Implementation Challenges

Implementing QEC in real quantum systems is no small feat. It requires highly precise control over qubits and quantum gates, as well as the ability to perform rapid and accurate measurements. Some of the practical challenges include:

• Decoherence: Maintaining the coherence of qubits over extended periods is crucial for effective QEC. Decoherence causes qubits to lose their quantum states, leading to errors.

• Quantum Gate Fidelity: High-fidelity quantum gates are essential for performing error detection and correction operations accurately. Any imperfections in these gates can introduce additional errors.

• Resource Overhead: QEC requires a significant number of physical qubits to protect a single logical qubit. Developing efficient QEC codes that minimize this overhead is an ongoing research focus.

Advanced QEC Techniques: Machine Learning and Beyond

Integrating machine learning techniques into QEC is an exciting area of research. Machine learning algorithms can analyze error patterns and predict the most likely errors, enabling more efficient and effective error correction. For example, reinforcement learning can optimize the sequence of quantum gates used in error correction protocols, reducing the overall error rate.

The ultimate goal of QEC research is to achieve fault-tolerant quantum computing, where quantum computations can be performed reliably despite the presence of errors. This requires developing QEC codes that can handle a wide range of error types and rates, as well as implementing these codes in practical quantum systems. Fault-tolerant quantum computing will enable us to harness the full power of quantum computers for solving complex problems that are currently beyond the reach of classical computers.

Why Quantum Error Correction Matters

You might be wondering, why go through all this trouble? The potential benefits of quantum computing are enormous. Imagine a world where we can solve complex optimization problems, develop new drugs with unprecedented precision, or simulate complex molecular interactions in a fraction of the time it takes today. Quantum computing promises to revolutionize fields from cryptography to material science, but only if we can ensure the accuracy of our computations.

QEC is the foundation that will support these breakthroughs. Without effective error correction, the power of quantum computers would be severely limited by the high error rates of qubits. By mastering QEC, we unlock the full potential of quantum computing, paving the way for practical, large-scale quantum systems.

Let's take a look at some potential real-world applications of quantum computing that could be unlocked with effective QEC:

• Cryptography: Quantum computers have the potential to break current cryptographic algorithms, making it essential to develop new, quantum-resistant cryptographic methods. QEC ensures that quantum computations for cryptographic purposes are accurate and reliable.

• Drug Discovery: Quantum computers can simulate molecular interactions at an unprecedented level of detail, potentially leading to the discovery of new drugs and treatments. QEC is crucial for maintaining the accuracy of these simulations.

• Optimization Problems: Many real-world problems, such as supply chain management and financial modeling, involve complex optimization. Quantum computers can solve these problems more efficiently, provided QEC ensures the reliability of the computations.

Wrapping Up

Quantum Error Correction might not be the flashiest topic, but it’s one of the most critical pieces of the quantum puzzle. It's the technology that ensures our quantum computations remain accurate and reliable, despite the inherent fragility of qubits. As we continue to explore the quantum frontier, understanding and improving QEC will be key to realizing the full potential of quantum computing.

So, stay tuned for more deep dives into the fascinating world of quantum mechanics and computing. Next up, we'll explore the wonders of quantum entanglement and how it powers quantum teleportation and beyond. Until then, keep those quantum questions coming, and let’s keep unraveling the mysteries of the quantum world together.

For those of you who want to dig deeper into Quantum Error Correction, here are some resources that helped shape my understanding:

• "Quantum Error Correction" by Daniel Gottesman: A foundational paper on the principles of QEC.

• "Quantum Computation and Quantum Information" by Michael A. Nielsen and Isaac L. Chuang: A comprehensive textbook covering all aspects of quantum computing, including QEC.

• YouTube Channels like Qiskit and minutephysics, which offer accessible explanations of quantum computing concepts.

• Research Papers: Look into recent papers on arXiv for the latest developments in QEC techniques and applications.

I'd like to remind everyone that I'm still very much a newbie in the field of Quantum Technology. In fact, calling myself a newbie might be an understatement. I'm here to share what I've learned so far on my journey to grasp the complexities of Quantum Mechanics and Quantum Computing.

Until next time!